L’introduction de modèles de machine learning complexes
Actuellement, dans l’univers de la data scienceQu'est-ce que la Data Science ? La Data Science, ou science des données, est une discipline interdisciplinaire qui utilise des méthodes scientifiques, des processus, des algorithmes et des systèmes pour extraire des connaissances et des insights à partir de données, qu'elles soient structurées ou no... More et plus précisément du machine learning, quand une entreprise souhaite employer des algorithmes supervisés, c’est-à-dire pour prédire l’appétence ou l’attrition de ses clients, la souscription ou le remboursement d’un produit bancaire, etc., les algorithmes classiques tels que les arbres de décision ou la régression logistique ne suffisent plus à atteindre les niveaux de précision exigés. Des nouvelles méthodes comme XGBoost [1] atteignent des niveaux de performance bien plus élevés que ces méthodes ; sur une comparaison avec 165 jeux de données [2], la régression logistique est plus performante dans seulement 5% et les arbres dans 2% des cas.
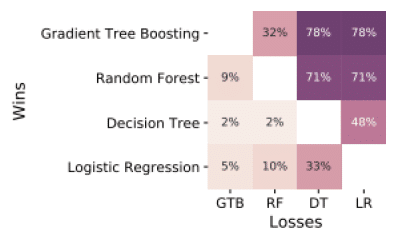
Comparaison d’algorithmes sur 165 jeux de données. Source [2]
Ces nouvelles méthodes sont plus efficaces pour plusieurs raisons :
- Elles prennent en compte plus efficacement les relations non linéaires ou non monotones entre une variable explicative et la cible à prédire.
- Elles savent bien gérer les phénomènes d’interactions entre variables.
- Elles améliorent le biais ou la variance de modèles simples en intégrant une dizaine voire une centaine de ces modèles par boosting ou par bagging.
Un besoin en interprétabilité croissant
Le trade-off avec ces nouveaux modèles est qu’en gagnant en performance, nous perdons en interprétabilité.
L’interprétabilité d’un modèle, que nous pouvons définir comme la capacité à comprendre les raisons d’une décision d’un modèle, est nécessaire pour plusieurs raisons :
- Le data scientist, auteur du modèle, doit comprendre les relations que le modèle a trouvées. Cela lui permet de communiquer les résultats, vérifier l’intuition des experts métiers (voire la sienne !) ou encore de débugger son modèle.
- De plus, les équipes métiers qui utiliseront le résultat du modèle doivent avoir confiance en sa performance et comprendre ce qui fait son utilité. Un modèle qui n’est pas compris ni éprouvé sera malheureusement rarement utilisé…
- Plus important encore, dans certains domaines d’application telle que la banque, le besoin d’interprétabilité est nécessaire pour le valider en interne. Cela est également essentiel pour se conformer aux exigences réglementaires (ACPR, AMF, BCE).
- Enfin, même si les conséquences de la réglementation RGPDQu'est-ce que le RGPD (Règlement Général sur la Protection des Données) ? Si vous travaillez de près ou de loin avec la donnée, le sigle RGPD (Règlement Général sur la Protection des Données) fait sans doute partie de votre quotidien, parfois perçu comme une contrainte, mais de plus en plus comme u... More sur l’utilisation de ces modèles en entreprise ne sont pas définies, il ne peut être qu’être conseillé d’être prudent sur ces exigences de transparence.
Les méthodes d’interprétabilité
Les différentes méthodes d’interprétabilité peuvent être définies selon 3 axes :
- Les approches globales VS locales. Le 1e type donne une interprétation pour tous les individus en même temps. Le second la donne pour un ou quelques individus.
- Les approches a priori VS a posteriori. La 1e concerne une méthode qui doit être employée avant la création du modèle. La 2nde doit être employée après. Une méthode a posteriori est préférable puisqu’il n’est pas toujours possible d’accéder à toutes les étapes de création du modèle (cas d’une validation externe par exemple).
- Les approches model-agnostic VS liées au modèle. La 1e correspond aux méthodes qui ne dépendent pas du type de modèle choisi. La 2nde est dépendante du modèle utilisé. La 1e est préférable parce qu’elle s’appliquera dans tous les domaines et pour toutes les problématiques.
Voici un tableau récapitulant les méthodes les plus importantes, classées selon les 3 axes :
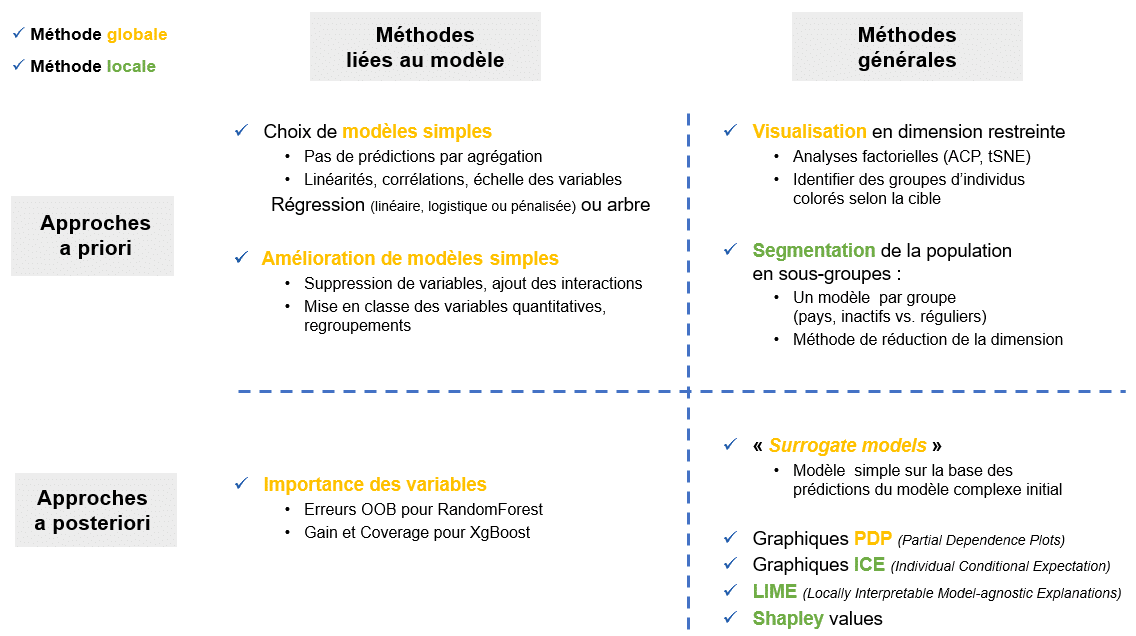
Descriptif de nombreuses méthodes selon 3 axes
Présentons maintenant 3 méthodes que nous pensons à Avisia comme étant les plus prometteuses.
Les graphiques ICE et PDP
Ces deux graphiques permettent d’inspecter la relation entre une variable explicative (voire deux) et le phénomène à expliquer pour lequel nous calculons des prédictions. Le procédé pour ICE (Individual Conditional Expectations [3]) est le suivant :
- Pour un individu donné, faire varier la valeur de la variable explicative à inspecter (afin qu’elle prenne toutes les valeurs possibles),
- Récupérer pour toutes ces nouvelles valeurs la prédiction associée,
- Répéter ce processus pour tous les individus et tracer les courbes.
Le graphique PDP (Partial Dependance Plot [4]) n’est que la moyenne des courbes individuelles pour toutes les valeurs de la variable.
Voici un exemple avec les données et le modèle XGBoost dont la description des variables et les codes de création sont en annexe :
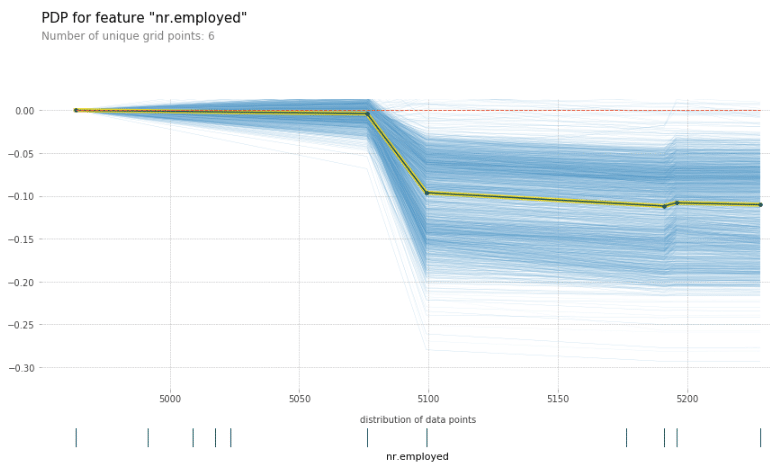
Code et graphique ICE/PDP pour la variable nr.employed
Le fait d’analyser le lien entre variable explicative et cible avant la création du modèle est moins robuste que les méthodes PDP & ICE, car nous ne prendrions pas en compte les effets d’interaction entre toutes les variables explicatives. Pour la variable nr.employed utilisée, nous voyons que les valeurs plus faibles ont un impact similaire, alors que des valeurs supérieures à 5100 ont un impact négatif. La relation semble similaire pour tous les individus. Note : la ligne jaune et noire correspond au PDP.
Les valeurs de Shapley
Les valeurs de Shapley empruntent à la théorie des jeux et représentent, pour un individu, la contribution de la valeur d’une variable à la prédiction de cet individu. La contribution de toutes les variables représente la différence entre la prédiction individuelle et la prédiction moyenne (tous les individus).
Code et graphique Shapley pour un individu
Le graphique nous montre que pour cet individu, la prédiction est bien inférieure à la prédiction moyenne. Cela est surtout dû aux variables emp.var.rate et duration, qui tirent la prédiction vers 0. L’influence de la variable nr.employed est cohérente avec le graphique PDP ci-dessus.
Note : la probabilité prédite de 0,2% s’obtient en utilisant la fonction sigmoïde au point -6,23.
La méthode permet aussi, entre autres, d’avoir l’importance des variables dans le modèle, de manière fiable :
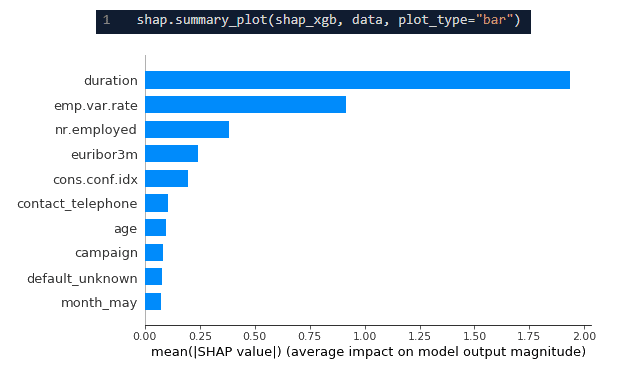
Code et graphique d’importance des variables par les valeurs de Shapley
LIME
La méthode LIME [5] consiste à expliquer la prédiction d’un individu par un modèle simple (régression L1 pondérée), et ce uniquement pour les individus dans son voisinage (qui lui sont semblables). En effet, si un modèle peut être globalement complexe, il sera localement plus simple.
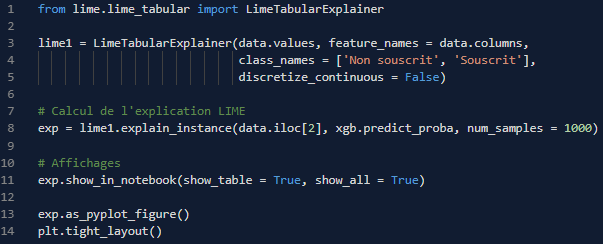
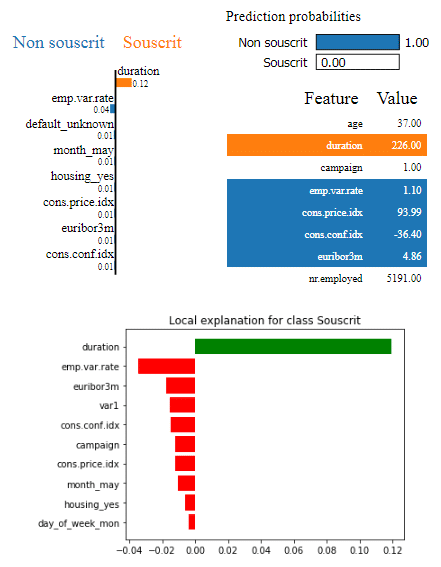
Code et graphique LIME pour un individu
Différents graphiques sont possibles en fonction des affinités ! Dans tous les cas, pour cet individu (le même que pour Shapley), nous voyons que, malgré sa probabilité proche de 0, la variable duration a eu le plus d’importance et a eu tendance à augmenter la probabilité finale. Cette analyse est en contradiction avec la méthode Shapley ; c’est dû à trois raisons, qui peuvent faire la faiblesse de LIME :
- La méthode LIME ne montre uniquement que ce qui a joué localement dans la prédiction, ce qui peut être différent de globalement (ce qui est le cas de Shapley),
- LIME est dépendant du choix du voisinage et peut être instable,
- Si localement le modèle reste complexe, alors le modèle local simple ne sera pas une bonne approximation du modèle global.
Avantages et inconvénients des méthodes
Avantages
- PCP & ICE : interprétation intuitive et causale du modèle (« si ma variable change pour cette valeur, l’impact sera celui-ci », ce qui n’est pas possible avec Shapley),
- PDP & ICE : la méthode est simple et facile à utiliser, et se généralise à 2 variables explicatives,
- PDP & ICE : le graphique ICE (mais pas PDP) peut mettre à jour des effets hétérogènes pour des individus semblables.
- Shapley : il est possible de savoir ce qui a exactement causé une prédiction d’un individu,
- Shapley : la théorie qui supporte cette méthode est solide, et elle possède des propriétés de justesse des résultats, contrairement aux autres (LIME, importance des variables),
- Shapley : la méthode permet aussi d’avoir des graphiques d’importance des variables (avec le sens de la relation) ainsi que des graphiques type PDP (influence d’une variable sur la cible).
- LIME : l’explication donnée est sparse, c’est-à-dire qu’elle utilise peu de variables,
- LIME : la méthode est utilisable pour des données textuelles ou sur des images !
Inconvénients
- PCP & ICE : comme pour Shapley, des corrélations entre variables peuvent engendrer la création de points incohérents (exemple : si on dispose des variables explicatives taille et poids, on risque de créer des points avec taille = 2m et poids = 40kg),
- PCP & ICE : il serait utile de rajouter la distribution de la variable, parce qu’une zone du graphique peut concerner très peu d’individus.
- Shapley : le calcul des contributions, s’il est exhaustif, peut être très long à calculer : c’est pour ça que les implémentations R/Python utilisent des approximations.
- LIME : comme vu avant, le choix du voisinage et le paramétrage de LIME peut donner des résultats instables et pas suffisamment fidèles.
L’interprétabilité à l’ère de l’IA Générative : SHAP appliqué aux LLM
Si ces méthodes ont fait leurs preuves sur des données tabulaires, l’essor fulgurant des Grands Modèles de Langage (LLMQu'est-ce qu'un Large Language Model (LLM) ? Si vous avez testé des outils d'IA conversationnelle récemment, alors vous avez directement interagi avec ce qu'on appelle un Large Language Model. Derrière ce terme se cache une réalité technologique fascinante. Concrètement, il s'agit d'un système d'int... More) depuis quelques années a poussé la recherche en XAIQu'est-ce que l'Explainable AI (XAI) ? Si vous travaillez dans la data, vous avez forcément déjà été confronté à l'effet "boîte noire". Vous développez un modèle de Deep Learning ultra-performant, les scores de précision s'envolent, mais au moment de le passer en production, le métier freine des qua... More à s’adapter. Aujourd’hui, des concepts dérivés de Shapley sont utilisés pour évaluer l’importance de chaque « token » (mot ou sous-partie de mot) dans le prompt d’un utilisateur, afin de comprendre pourquoi un LLM a généré une réponse spécifique plutôt qu’une autre. Bien que ces modèles comportent des milliards de paramètres, l’application de méthodes d’attribution permet aux développeurs de détecter des biais dans la génération de texte, de fiabiliser les architectures RAGQu'est-ce que le RAG - Retrieval Augmented Generation ? Le Retrieval Augmented Generation (RAG) est une technique avancée d'intelligence artificielle qui combine la recherche d'informations (retrieval) avec la génération de texte (generation) pour fournir des réponses précises et contextuellement pe... More, et d’assurer une meilleure traçabilité algorithmique indispensable pour la mise en production.
Conclusion
Les exigences réglementaires et d’utilisation en contexte d’entreprise demandent de plus en plus d’avoir des modèles à la fois simples et performants. Pouvoir interpréter facilement et efficacement des modèles complexes en facilite l’emploi. Cela doit être un outil dans la panoplie du data scientist moderne. Grâce aux méthodes présentées dans cet article, l’interprétabilité et la performance deviennent accessibles. La méthode la plus utile est la valeur Shapley. Elle permet de déterminer à la fois ce qui joue pour la prédiction d’un individu (sens et importance), de tous les individus (importance des variables) et plus spécifiquement pour une variable ou l’interaction de deux variables. La méthode PDP peut en être complémentaire.
Vous développez des modèles de Machine Learning ou déployez des solutions basées sur l’IA GénérativeQu'est-ce que l'IA Générative ? L'IA Générative est une sous-branche de l'IA. Elle se concentre sur la création de nouveaux contenus (textes, images, vidéos...) à partir des données d'entraînement. Les modèles d'IA générative sont capables de générer de nouvelles données similaires aux données sur l... More, mais vous butez sur l’explicabilité de vos algorithmes face aux nouvelles réglementations (AI ActQu'est-ce que l'IA Act ? Le 13 mars 2024, le Parlement européen a adopté l’IA Act (ou Règlement sur l'Intelligence Artificielle), marquant une étape historique : il s’agit du premier cadre juridique complet au monde visant à encadrer le développement, la mise sur le marché et l’utilisation des systè... More) ?
Contactez nos experts AVISIA pour auditer, sécuriser et mettre en production des modèles performants, éthiques et 100% interprétables.
Annexe
Le jeu de données est une légère modification de celui disponible sur l’archive UCI ML [6]. Le but est de prédire si des clients d’une banque vont effectuer un dépôt à terme après des contacts de marketing direct. Les créateurs de ces données indiquent que la variable duration est fortement explicative du dépôt.
Voici le code utilité pour le traitement des données et le modèle XGBoost :
# Import
import pandas as pd
data = pd.read_csv(‘bank-additional-full-atelier.csv’)
# Pretraitement
y = data[‘y’]
del data[‘y’]
# One hot encoding
data_car = data.select_dtypes(‘object’)
data_num = [x for x in data if x not in data_car]
data_num = data[data_num]
data_dummies = pd.get_dummies(data_car, drop_first = True
data = pd.concat([data_num, data_dummies], axis = 1)
# Modélisation XGBoost
import xgboost
xgb = xgboost.XGBClassifier(learning_rate = 0.03, n_estimators = 500, max_depth = 4, objective = ‘binary:logistic’)
xgb.fit(data.valyes, y)
Bibliographie
[1] Chen T., Guestrin C. (2016). https://arxiv.org/abs/1603.02754v1
[2] Olson R. S., La Cava W., Mustahsan Z., Varik A., and Jason H. Moore (2018). Data-driven advice for applying machine learning to bioinformatics problems, https://psb.stanford.edu/psb-online/proceedings/psb18/olson.pdf
[3] Goldstein A., Kapelner A., Bleich J., Pitkin E. (2013). Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation, https://arxiv.org/abs/1309.6392
[4] Friedman J. H. (2001). Greedy function approximation: A gradient boosting machine, https://statweb.stanford.edu/~jhf/ftp/trebst.pdf
[5] Ribeiro M. T., Singh S., Guestrin C. (2016). Why should I trust you?: Explaining the predictions of any classifier, https://www.kdd.org/kdd2016/papers/files/rfp0573-ribeiroA.pdf
[6] Moro S., Cortez P., Rita P. (2014). A Data-Driven Approach to Predict the Success of Bank Telemarketing https://archive.ics.uci.edu/ml/datasets/bank+marketing
